4. Beam Elements - Beam3D
Beam elements are a specialization of a volume element in which two directions, the beam cross section, may be assumed to be small with respect to the beam axis.
The Beam3D module is used to simulate 3D beam elements. Beam elements are one-dimensional elements in 3D space which support axial deformation, bending and torsion. In addition Beam3D supports the flexibility due to transverse shear deformation.
The methods associated with a Beam3D object are the following.
Begin and end an instance of an object, generic object functions
vfe_Beam3DBegin()- create an instance of a Beam3D objectvfe_Beam3DEnd()- destroy an instance of a Beam3D objectvfe_Beam3DError()- return Beam3D object error flag
Attributes and Parameters
vfe_Beam3DSetHistPtr()- set pointers to material historyvfe_Beam3DSetLocalSystem()- set stress axes directionvfe_Beam3DSetObject()- set attribute objectvfe_Beam3DSetParamd()- set element formulation parametersvfe_Beam3DSetParami()- set element formulation parametersvfe_Beam3DSetPropPtr()- set pointer to element nodal propertiesvfe_Beam3DSetTopology()- set input element topologyvfe_Beam3DDirCos()- compute beam local direction cosines
Degree of Freedom and Integration Information
vfe_Beam3DDofMap()- query element degree of freedom mapvfe_Beam3DNumDof()- query number of element degrees of freedomvfe_Beam3DNumIntPnt()- query number of element integration pointsvfe_Beam3DSetPins()- set pin flagsvfe_Beam3DSixDof()- gather nodal displacements and rotations
Structural analysis computations
vfe_Beam3DDistLoad()- distributed load vector.vfe_Beam3DElemLoad()- body force vectorvfe_Beam3DGeomStiff()- geometric stiffness matrixvfe_Beam3DInitHist()- initialize material historyvfe_Beam3DMass()- consistent mass matrixvfe_Beam3DMassDiag()- diagonal mass matrixvfe_Beam3DReact()- reaction vectorvfe_Beam3DReactStiff()- reaction vector, stiffness matrixvfe_Beam3DStiff()- linear stiffness matrixvfe_Beam3DStrsAdapt()- stress based error analysisvfe_Beam3DStrsStrn()- resultant stress and strain/curvaturevfe_Beam3DStressStrain()- three-dimensional stress and strainvfe_Beam3DUpdateDofs()- update dofs for large-rotation problems
4.1. Element Geometry
The basic beam element geometry is defined by the node coordinates of the
beam reference axis.
The beam section is defined by the node offsets of the beam centroidal
axis, beam section properties and beam node normals.
These beam section properties which are set using vfe_Beam3DSetPropPtr()
are illustrated below in Figure 4-2.
Additional beam section properties may be set such as area, moments of
inertia, torsional constant and shear center offsets.
Other element quantities which may be set using
this function are
beam temperature and effective shear factor.
If the node offsets are zero, the beam centroidal axis is coincident
with the beam reference axis.
In general, large centroidal axis offset values,
which are much greater than the beam section dimensions, should be avoided.
By default the beam section is perpendicular to the tangent along the
beam reference axis with the orientation of the section defined by
a prescription specified by vfe_Beam3DSetLocalSystem().
The user
may optionally
enter node normals to specifically define the orientation of the
beam cross section. These user defined normals allow for beam section
orientations which are not perpendicular to the beam reference axis
and override the prescription for the
node normals specified in vfe_Beam3DSetLocalSystem().
If the both the node normal y and normal z
are set using vfe_Beam3DSetPropPtr() the beam section lies in the plane
defined by the node normals. The node normal z is recomputed to be orthogonal
to the normal y. If only the normal y is set then the normal z is computed
to be orthogonal to the centroidal axis and the node normal y.
Beam properties such as area, offsets,
moments of inertia, shear center offsets, etc. are always measured in the
plane perpendicular to the beam reference axis regardless of the direction of
the beam node normals.
The element natural coordinate, r, is tangent to the the beam centroidal axis.
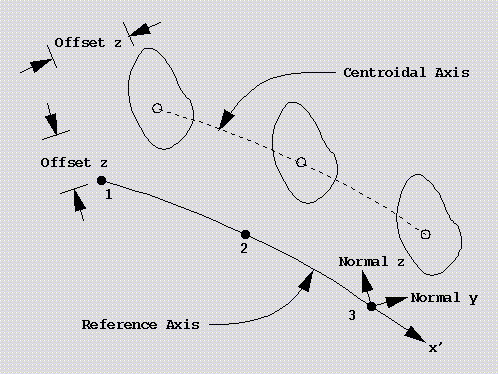
Figure 4-2, Geometry for 3 Node 3D Beam Element
The exact specification of the beam section which couples element
and primitive material properties,
is managed using the BeamProp module.
The BeamProp module provides for general integrated beam sections
vfe_BeamPropSetIntegrate() as well as preintegrated beam sections
input as general section area properties, vfe_BeamPropSetSection(),
or as a general matrix,
vfe_BeamPropSetMatrix(), relating centroidal axis
strains and curvatures to
stress and moment resultants.
For general integrated and general area beam sections the BeamProp module
allows a primitive material, such as defined by the LinMat
module, to be specified.
Note that when using the general integrated beam section defined by
vfe_BeamPropSetIntegrate(),
the actual distance of the beam section integration point from the
centroidal axis is computed internally by multiplying the integration point
coordinates input in vfe_BeamPropSetIntegrate() by one-half of the
thicknesses specified using vfe_Beam3DSetPropPtr().
Use the function
vfe_Beam3DStrsAdapt() to aid in computing element strain energy, strain
energy error and other useful quantities to aid in solution error estimation
and mesh adaptation.
Pin flags can be set at either of the beam’s ends with vfe_Beam3DSetPins().
Degrees of freedom marked with a pin flag are not transmitted to
neighboring elements. Every degree of freedom marked with a pin flag creates
an additional internal degree of freedom in the element. If large rotations
are used then the degrees of freedom in the element must be updated using
vfe_Beam3DUpdateDofs(), otherwise updated degrees of freedom are simply the
addition of the degrees of freedom at the beginning of the step and the
incremental values. If pin flags are defined, the element degrees of
freedom may be recovered using vfe_Beam3DSixDof().
4.2. Function Descriptions
The currently available Beam3D functions are described in detail in this section.
-
vfe_Beam3D *vfe_Beam3DBegin(void)
create an instance of a Beam3D object
Create an instance of a Beam3D object. Memory is allocated for the object private data and the pointer to the object is returned. Default topology is the 2-noded element with isoparametric technology.
Destroy an instance of a Beam3D object using
void vfe_Beam3DEnd (vfe_Beam3D *beam3d)
Return the current value of a Beam3D object error flag using
Vint vfe_Beam3DError (vfe_Beam3D *beam3d)
- Returns
The function returns a pointer to the newly created Beam3D object. If the object creation fails, NULL is returned.
-
void vfe_Beam3DEnd(vfe_Beam3D *p)
destroy an instance of a Beam3D object
-
Vint vfe_Beam3DError(vfe_Beam3D *p)
return the current value of a Beam3D object error flag
-
void vfe_Beam3DSetObject(vfe_Beam3D *p, Vint objecttype, Vobject *object)
set attribute object
Set a pointer to an attribute object. Users must supply a MatlFun object prior to computing any quantity that requires a material model definition.
- Errors
SYS_ERROR_OBJECTTYPEis generated if an improper objecttype is specified.
- Parameters
p – Pointer to Beam3D object.
objecttype – The object type identifier
x=VFE_MATLFUN MatlFun object
object – Pointer to the object to be set.
-
void vfe_Beam3DSetParami(vfe_Beam3D *p, Vint type, Vint iparam)
set element formulation parameters
Set element technology and formulation parameters.
The basic element technology is set with the
VFE_TECHparameter. The Kirchhoff technology assumes a cubic variation of displacement transverse to the beam axis and is only available in a pre-integrated formulation and a two node topology. By defaultVFE_TECHis set toVFE_TECH_ISOP.Toggle large rotations using
VFE_LARGEROTATION. By defaultVFE_LARGEROTATIONis set toSYS_OFF.The addition of rotary inertias to the element mass matrix is set with the
VFE_ROTINERTIAparameter. By defaultVFE_ROTINERTIAis set toSYS_OFF.The parameter
VFE_TEMPMATLAVGtoggles the method for computing the temperature used for evaluating temperature dependent material properties. If enabled, the temperature used for temperature dependent material properties is the average of the element node point temperatures. If disabled, the temperature is isoparametrically interpolated from the node point temperatures at each element integration point. By defaultVFE_TEMPMATLAVGis set toSYS_ON.- Errors
SYS_ERROR_ENUMis generated if an improper type is specified.SYS_ERROR_VALUEis generated if an improper iparam is specified.
- Parameters
p – Pointer to Beam3D object.
type – Type of formulation parameter to set
x=VFE_TECH Element technology =VFE_LARGEROTATION Toggle for large rotations =VFE_ROTINERTIA Enable rotary inertias =VFE_TEMPMATLAVE Average material temperature flag
iparam – Integer parameter value.
x=VFE_TECH_ISOP Mindlin isoparametric technology =VFE_TECH_KIRCHHOFF Kirchhoff technology =VFE_TECH_ENHANCED Enhanced technology =SYS_OFF Disable =SYS_ON Enable
-
void vfe_Beam3DSetParamd(vfe_Beam3D *p, Vint type, Vdouble dparam)
set element formulation parameters
Set element formulation parameters.
Use
VFE_MAXPROJANGto set the maximum angle in degrees between the beam tangent at an element integration point and the beam tangent at a node. By defaultVFE_MAXPROJANGis set to 90. degrees.Use
VFE_ADDEDMASSto add non-structural mass/length to the beam element. By defaultVFE_ADDEDMASSis set to 0..- Errors
SYS_ERROR_ENUMis generated if an improper type is specified.SYS_ERROR_VALUEis generated if an improper dparam is specified.
- Parameters
p – Pointer to Beam3D object.
type – Type of formulation parameter to set
x=VFE_MAXPROJANG Maximum nodal projection angle =VFE_ADDEDMASS Additional mass/length
dparam – Double precision parameter value.
-
void vfe_Beam3DSetTopology(vfe_Beam3D *p, Vint maxi)
set element topology
Specify the topology of a 3D beam element. If maxi is set to 3 then a quadratic element form is assumed.
- Errors
SYS_ERROR_VALUEis generated if an improper maxi is specified.
- Parameters
p – Pointer to Beam3D object.
maxi – The number of points along the i direction. If maxi = 0 then the linear Serendipity element form of the specified shape is assumed.
-
void vfe_Beam3DSetPropPtr(vfe_Beam3D *p, Vint type, Vdouble *propptr)
set pointer to element nodal properties
Set a pointer to the start of a specified type of element nodal properties. Note that the properties are not copied by this function, only the pointer itself is copied. If a property pointer is not set the element assumes a default value for the associated property. By default the temperature is 0., the thicknesses are 2., the offsets are 0., the area is 4., and the effective shear factors are 5/6. By default the reference temperature is 0.
- Errors
SYS_ERROR_ENUMis generated if an improper type is specified.
- Parameters
p – Pointer to Beam3D object.
type – Type of element property
x=VFE_PROP_TEMPERATURE Temperatures =VFE_PROP_TEMPREF Reference temperatures =VFE_PROP_THICKNESSY Thicknesses in y' =VFE_PROP_THICKNESSZ Thicknesses in z' =VFE_PROP_OFFSETY Offsets in y' =VFE_PROP_OFFSETZ Offsets in z' =VFE_PROP_NORMALY Normals in y' =VFE_PROP_NORMALZ Normals in z' =VFE_PROP_AREA Areas =VFE_PROP_IYY Moments of inertia about y' =VFE_PROP_IZZ Moments of inertia about z' =VFE_PROP_IYZ Products of inertia =VFE_PROP_J Torsional constants =VFE_PROP_KSY Effective shear factor in y' =VFE_PROP_KSZ Effective shear factor in z' =VFE_PROP_DSY Shear center offsets in y' =VFE_PROP_DSZ Shear center offsets in z'
propptr – Pointer to start of element nodal properties
-
void vfe_Beam3DReactStiff(vfe_Beam3D *p, Vdouble x[][3], Vdouble u[], Vint kflag, Vdouble r[], Vdouble k[])
reaction vector, stiffness matrix
Compute the reaction vector, r, and optionally the stiffness matrix, k, given the node coordinates, x, and the degree of freedom displacement vector, u. The lower triangle of the stiffness matrix is returned.
- Errors
SYS_ERROR_NULLOBJECTis generated if a MatlFun attribute object has not been set.SYS_ERROR_COMPUTEis generated if a negative Jacobian transformation is computed or the maximum nodal projection angle is exceeded.
- Parameters
p – Pointer to Beam3D object.
x – Array of node locations.
u – Degree of freedom vector of displacements
kflag – Flag to compute stiffness matrix, k
=SYS_OFF Do not compute stiffness matrix =SYS_ON Compute and return stiffness matrix
r – [out] Degree of freedom reaction vector
k – [out] Degree of freedom stiffness matrix
-
void vfe_Beam3DReact(vfe_Beam3D *p, Vdouble x[][3], Vdouble u[], Vdouble r[])
reaction vector
Compute the reaction vector, r, given the node coordinates, x, and the degree of freedom displacement vector, u.
- Errors
SYS_ERROR_NULLOBJECTis generated if a MatlFun attribute object has not been set.SYS_ERROR_COMPUTEis generated if a negative Jacobian transformation is computed or the maximum nodal projection angle is exceeded.
- Parameters
p – Pointer to Beam3D object.
x – Array of node locations.
u – Degree of freedom vector of displacements
r – [out] Degree of freedom reaction vector
-
void vfe_Beam3DInitHist(vfe_Beam3D *p)
initialize material history
Initialize the values of the history variables used in the underlying element or primitive material model for the element. This operation should be performed once for each element (at the first load or time step for example) to initialize the old history variables to reflect the initial configuration condition. If the number of history variables is zero, this function need not be called.
- Errors
SYS_ERROR_NULLOBJECTis generated if a MatlFun attribute object has not been set.
- Parameters
p – Pointer to Beam3D object.
-
void vfe_Beam3DStiff(vfe_Beam3D *p, Vdouble x[][3], Vdouble kl[])
linear stiffness matrix
Compute the linear stiffness matrix, kl, given the node coordinates, x. The lower triangle of the stiffness matrix is returned.
- Errors
SYS_ERROR_NULLOBJECTis generated if a MatlFun attribute object has not been set.SYS_ERROR_COMPUTEis generated if a negative Jacobian transformation is computed or the maximum nodal projection angle is exceeded.
- Parameters
p – Pointer to Beam3D object.
x – Array of node locations.
kl – [out] Degree of freedom stiffness matrix
-
void vfe_Beam3DGeomStiff(vfe_Beam3D *p, Vdouble x[][3], Vdouble u[], Vdouble kg[])
geometric stiffness matrix
Compute the geometric stiffness matrix, kg, given the node coordinates, x, and the degree of freedom displacement vector, u. The lower triangle of the geometric stiffness is returned.
- Errors
SYS_ERROR_NULLOBJECTis generated if a MatlFun attribute object has not been set.SYS_ERROR_COMPUTEis generated if a negative Jacobian transformation is computed or the maximum nodal projection angle is exceeded.
- Parameters
p – Pointer to Beam3D object.
x – Array of node locations.
u – Degree of freedom vector of displacements
kg – [out] Degree of freedom geometric stiffness matrix
-
void vfe_Beam3DStrsStrn(vfe_Beam3D *p, Vdouble x[][3], Vdouble u[], Vdouble strs[], Vdouble strn[])
resultant stress and strain/curvature
Compute nodal stress resultants and strains, strs and strn, given the node coordinates, x, and the degree of freedom displacement vector, u.
The stress resultants and strains/curvatures are computed in the beam local coordinate system. The convention used to generate local coordinate systems is specified using
vfe_Beam3DSetLocalSystem()or alternatively setting normal directions usingvfe_Beam3DSetPropPtr(). The actual direction cosine matrices of the beam local systems at the element output locations may be returned usingvfe_Beam3DDirCos().The strs is composed of 6 stress resultants and the strn is composed of 6 associated midsurface strains, twists and curvatures at each output location. The stress and strain values are ordered first by the 6 stress resultant or strain components followed by the the number of element nodes. For example, for a 2 node beam element a total of 6*2 = 12 stress resultant values will be returned in strs and 12 strain values returned in strn.
- Errors
SYS_ERROR_NULLOBJECTis generated if a MatlFun attribute object has not been set.SYS_ERROR_COMPUTEis generated if a negative Jacobian transformation is computed or the maximum nodal projection angle is exceeded.
- Parameters
p – Pointer to Beam3D object.
x – Array of node locations.
u – Degree of freedom vector of displacements
strs – [out] Array of nodal stress resultant
strn – [out] Array of nodal strains/curvatures
-
void vfe_Beam3DStressStrain(vfe_Beam3D *p, Vdouble x[][3], Vdouble u[], Vdouble strs[], Vdouble strn[], Vdouble stress[], Vdouble strain[])
three-dimensional stress and strain
Compute nodal stress resultants and strains, strs and strn, and the three-dimensional stresses and strains, stress and strain, given the node coordinates, x, and the degree of freedom displacement vector, u.
The stress resultants and strains/curvatures are the same as those obtained with
vfe_Beam3DStrsStrn(), and the same remarks regarding local coordinate systems apply.The three-dimensional stresses and strains are computed at a series of points in the beam’s cross section. The number of cross sectional points is obtained using
vfe_MatlFunNumStressStrain()and depend on the type of cross section used. See BeamProp for more details on each cross section type.- Errors
SYS_ERROR_NULLOBJECTis generated if a MatlFun attribute object has not been set.SYS_ERROR_COMPUTEis generated if a negative Jacobian transformation is computed or the maximum nodal projection angle is exceeded.
- Parameters
p – Pointer to Beam3D object.
x – Array of node locations.
u – Degree of freedom vector of displacements
strs – [out] Array of nodal stress resultant
strn – [out] Array of nodal strains/curvatures
stress – [out] Array of nodal three dimensional stresses at recovery points
strain – [out] Array of nodal three dimensional strains at recovery points
-
void vfe_Beam3DNumDof(vfe_Beam3D *p, Vint analysistype, Vint *nedofs)
query number of element degrees of freedom
Query for number of element degree of freedom nedofs. The number of degrees of freedom will generally be equal to the number of nodal degrees of freedom per node times the number of nodes plus the number of elemental degrees of freedom. Use
vfe_Beam3DDofMap()to return the location and type of each degree of freedom.- Errors
SYS_ERROR_ENUMis generated if an improper analysistype is specified.
- Parameters
p – Pointer to Beam3D object.
analysistype – The type of analysis
x=VFE_ANALYSIS_STRUCTURAL Structural analysis
nedofs – [out] Number of element degrees of freedom
-
void vfe_Beam3DDofMap(vfe_Beam3D *p, Vint analysistype, Vint loc[], Vint tag[])
query element degree of freedom map
Query for element degree of freedom map. The degree of freedom map consists of a location index, loc and type, tag for each degree of freedom used by the element.
The location index is either a positive node index into the element connectivity indicating a nodal freedom or a zero value indicating an elemental degree of freedom. The tag indicates the type of the degree of freedom. Tag values are one of a set of enumerated types which indicate whether the degree of freedom is a translation or rotation.
The length of the loc and tag vectors is equal to the number of element degrees of freedom. Use
vfe_Beam3DNumDof()to return the number of element degrees of freedom.- Errors
SYS_ERROR_ENUMis generated if an improper analysistype is specified.
- Parameters
p – Pointer to Beam3D object.
analysistype – The type of analysis
x=VFE_ANALYSIS_STRUCTURAL Structural analysis
loc – [out] Vector of degree of freedom locations
tag – [out] Vector of degree of freedom types
-
void vfe_Beam3DMass(vfe_Beam3D *p, Vdouble x[][3], Vdouble m[])
consistent mass matrix
Compute the consistent mass matrix, m, given the node coordinates, x. The lower triangle of the consistent mass is returned. Use
vfe_Beam3DMassDiag()to compute a diagonal mass matrix.- Errors
SYS_ERROR_NULLOBJECTis generated if a MatlFun attribute object has not been set.SYS_ERROR_COMPUTEis generated if a negative Jacobian transformation is computed or the maximum nodal projection angle is exceeded.
- Parameters
p – Pointer to Beam3D object.
x – Array of node locations.
m – [out] Degree of freedom consistent mass matrix
-
void vfe_Beam3DMassDiag(vfe_Beam3D *p, Vdouble x[][3], Vdouble md[])
diagonal mass matrix
Compute the diagonal mass matrix, md, given the node coordinates, x. The diagonal mass is returned as a degree of freedom length vector. Use
vfe_Beam3DMass()to compute a consistent mass matrix.- Errors
SYS_ERROR_NULLOBJECTis generated if a MatlFun attribute object has not been set.SYS_ERROR_COMPUTEis generated if a negative Jacobian transformation is computed or the maximum nodal projection angle is exceeded.
- Parameters
p – Pointer to Beam3D object.
x – Array of node locations.
md – [out] Degree of freedom diagonal mass vector
-
void vfe_Beam3DDistLoad(vfe_Beam3D *p, Vdouble x[][3], Vint enttype, Vint no, Vint loadtype, Vdouble q[], Vdouble f[])
distributed load vector
Compute the consistent degree of freedom loads given a distributed load, q along a 3D beam element edge. The vector q contains values for the load type for each node in the element. If the loadtype is
VFE_DISTLOAD_TRACthen q contains a vector traction at each element node. If the traction is applied to an edge the units are force/length. at each element node. Note that the input array of node locations, x, contains the coordinate locations for all nodes in the element. Correspondingly the output array of consistent degree of freedom loads, f, contains loads for all degrees of freedom in the element. The distributed loads for edges are in units of force per unit length.- Errors
SYS_ERROR_ENUMis generated if an improper enttype or loadtype is specified.SYS_ERROR_OPERATIONis generated if an invalid combination of enttype and loadtype is specified.SYS_ERROR_VALUEis generated if an improper no is specified.SYS_ERROR_COMPUTEis generated if a zero edge Jacobian is computed.
- Parameters
p – Pointer to Beam3D object.
x – Array of node locations.
enttype – Entity type on which load is applied
=SYS_EDGE Element edge
no – Element edge number, currently unused and ignored.
loadtype – Distributed load type
x=VFE_DISTLOAD_TRAC Load directed along vector
q – Vector of distributed load values
f – [out] Degree of freedom vector of consistent loads.
-
void vfe_Beam3DElemLoad(vfe_Beam3D *p, Vdouble x[][3], Vdouble q[][3], Vdouble f[])
body force vector
Compute the consistent degree of freedom body loads given acceleration load vector, q, on an element. The vector q contains an acceleration vector for for each node in the element. The output array of consistent degree of freedom loads, f, contains loads for all degrees of freedom in the element. The input element loads are in the units of force per unit mass. Note that the computation of consistent loads uses the material density.
- Errors
SYS_ERROR_COMPUTEis generated if a zero Jacobian is computed.
- Parameters
p – Pointer to Beam3D object.
x – Array of node locations.
q – Array of node accelerations
f – [out] Degree of freedom vector of consistent loads.
-
void vfe_Beam3DSetHistPtr(vfe_Beam3D *p, Vdouble *oldhist, Vdouble *newhist)
set pointers to material history
Set pointers to the start of the material history data at the previous step, oldhist and the current step newhist. This function is required when an underlying material model such as plasticity is used. Note that the material history data is not copied by this function, only the pointers themselves are copied. The number of double precision values required for the material history at a step is the number of history variables at an integration point times the total number of integration points in the element. The number of history variables depends on the underlying material model and may be queried using
vfe_MatlFunNumHist(). The total number of integration points is the product of the number of element integration points returned usingvfe_Beam3DNumIntPnt()and the number of history values returned usingvfe_MatlFunNumHist(). By default the pointers to the material history are NULL. If the number of history variables is zero, this function need not be called.- Parameters
p – Pointer to Beam3D object.
oldhist – Pointer to start of material history at previous step
newhist – Pointer to start of material history at current step
-
void vfe_Beam3DNumIntPnt(vfe_Beam3D *p, Vint analysistype, Vint *nepnts)
query number of element integration points
Query for number of element integration points nepnts.
- Errors
SYS_ERROR_ENUMis generated if an improper analysistype is specified.
- Parameters
p – Pointer to Beam3D object.
analysistype – The type of analysis
x=VFE_ANALYSIS_STRUCTURAL Structural analysis
nepnts – [out] Number of element integration points
-
void vfe_Beam3DSetLocalSystem(vfe_Beam3D *p, Vint type, Vdouble vec[], Vdouble angle)
set local coordinate system convention
Specify the convention to be used to construct the orientation of the beam element local x’,y’,z’ coordinate system with respect to the beam reference axis. This local system is computed at each integration point location on the beam axis and is assumed to be the coordinate system in which the material properties of the element at the integration point are expressed. For stress and strain computation for output using either
vfe_Beam3DStrsStrn()orvfe_Beam3DStressStrain(), the local coordinate system is evaluated at each output location and is the coordinate system in which the output stresses and strains at the output location are expressed.The x’ axis is always constructed to be tangent to the beam reference axis. The orientation of the y’ and z’ axes perpendicular to the beam reference axis is determined by type. The vec array is only used if the specified type requires position or direction vectors. An additional rotation of the y’,z’ axes about the x’ axis can be specified with angle. By default the local system convention is
SYS_ELEMSYS_STANDARDwith angle set to 0.For a description of element coordinate systems, type, and associated orientation vector data, please see Element Coordinate Systems
- Errors
SYS_ERROR_ENUMis generated if an improper type is input.
- Parameters
p – Pointer to Beam3D object.
type – Local system convention
vec – Orientation vector data
angle – Angle to rotate beam y’,z’ axes about the beam x’ axis in degrees.
-
void vfe_Beam3DDirCos(vfe_Beam3D *p, Vdouble x[][3], Vdouble u[], Vdouble tm[][3][3])
compute beam local direction cosines
Compute the direction cosine matrices of the element local coordinate system. For stress and strain computation the local coordinate system at each stress output location is the coordinate system in which the output stresses and strains at the location using either
vfe_Beam3DStrsStrn()orvfe_Beam3DStressStrain()are expressed. Given that X’,Y’ and Z’ are three orthonormal vectors indicating the direction of the local coordinate axes in the global coordinate system (x,y,z), then the direction cosine matrix, tm for this local coordinate system is defined as:The local coordinate system is determined by the local system convention set usingtm[0][0] = X'x tm[0][1] = X'y tm[0][2] = X'z tm[1][0] = Y'x tm[1][1] = Y'y tm[1][2] = Y'z tm[2][0] = Z'x tm[2][1] = Z'y tm[2][2] = Z'z
vfe_Beam3DSetLocalSystem()or alternatively the normals in the beam y’ and z’ directions usingvfe_Beam3DSetPropPtr().The element degrees of freedom, u, are only required if large rotations have been enabled. Otherwise this argument is ignored.
- Parameters
p – Pointer to Beam3D object.
x – Array of point locations defining beam surface.
u – The element degrees of freedom
tm – [out] Array of direction cosine matrices at the element nodes.
-
void vfe_Beam3DStrsAdapt(vfe_Beam3D *p, Vdouble x[][3], Vdouble u[], Vdouble strss[], Vdouble *setot, Vdouble *seerr, Vdouble *hsize, Vdouble *order, Vdouble *d)
stress based error analysis
Compute the element total strain energy, setot, and strain energy error, seerr, given the element displacements, u, and an estimate of the exact nodal stress resultants, strss. In addition useful quantities such as the characteristic length, effective polynomial order and dimension of the element are returned. The element dimension, d, is 1. These quantities are useful for computing new characteristic element length for mesh adaptation.
- Errors
SYS_ERROR_NULLOBJECTis generated if a MatlFun attribute object has not been set.SYS_ERROR_COMPUTEis generated if a negative Jacobian transformation is computed or the maximum nodal projection angle is exceeded.
- Parameters
p – Pointer to Beam3D object.
x – Array of node locations.
u – Degree of freedom vector of displacements
strss – Array of recovered nodal stresses
setot – [out] Total strain energy
seerr – [out] Strain energy error
hsize – [out] Characteristic length
order – [out] Effective polynomial order
d – [out] Dimension
-
void vfe_Beam3DSetPins(vfe_Beam3D *p, Vint npins1, Vint tags1[], Vint npins2, Vint tags2[])
set pin flags
Sets pin flags at either end of the beam. If a linear beam then the second node is node 2; if a quadratic beam then the second node is the third beam.
- Errors
SYS_ERROR_ENUMis generated if an improper tags1 or tags2 contains entries other thanSYS_DOF_TX,SYS_DOF_TY,SYS_DOF_TZ,SYS_DOF_RX,SYS_DOF_RY, orSYS_DOF_RZ.
- Parameters
p – Pointer to Beam3D object.
npins1 – Number of pin flags set on first node
tags1 – List of npins1 degrees of freedom pinned on first node
npins2 – Number of pin flags set on second node
tags2 – List of npins2 degrees of freedom pinned on second node
-
void vfe_Beam3DUpdateDofs(vfe_Beam3D *p, Vdouble x[][3], Vdouble un[], Vdouble uinc[], Vdouble un1[])
update dofs for large-rotation problems
Compute the updated degrees of freedom at the end of a step given the initial and incremental values. For linear analysis the updated dofs are simply the sum of the un and uinc; however, if large rotations are used, the rotation dofs at the end of the step require special treatment.
- Parameters
p – Pointer to Beam3D object.
x – Array of point locations defining beam surface.
un – Dofs at the beginning of the step
uinc – Incremental dofs computed at the step
un1 – [out] Dofs at the end of the step
-
void vfe_Beam3DSixDof(vfe_Beam3D *p, Vdouble x[][3], Vdouble u[], Vdouble sixdof[])
gather nodal displacements and rotations
Gathers the nodal displacements and rotations for the element. This function is needed in case pin flags are set. In this case the incoming degrees of freedom are usually those shared with all elements connected through the node. The element’s displacement and rotation degrees of freedom require an internal transformation performed by this function.
- Parameters
p – Pointer to Beam3D object.
x – Array of point locations defining beam surface.
u – The element degrees of freedom
sixdof – [out] Global displacements and rotations for each node
